Özet: Bu makalede, kuantum fiziğinin en çarpıcı kavramlarından biri olan Schrödinger’in Kedisi düşünce deneyine teknik bir bakış sunulmakta, bu deneyin temelini oluşturan Schrödinger Denklemi ayrıntılı olarak incelenmektedir. Aynı zamanda, bu denklemin gerçek dünyadaki uygulamalarına örnekler verilerek, teorik fizikten teknolojiye uzanan etkileri tartışulmaktadır. Kuantum süreçlerin klasik sistemlerle etkileşimi, yorum farklılıkları, dalga mekaniği yaklaşımı ve deneysel gelişmeler de ele alınmaktadır.
Schrödinger’in Kedisi : Kuantum Süperpozisyonunun Paradoksu
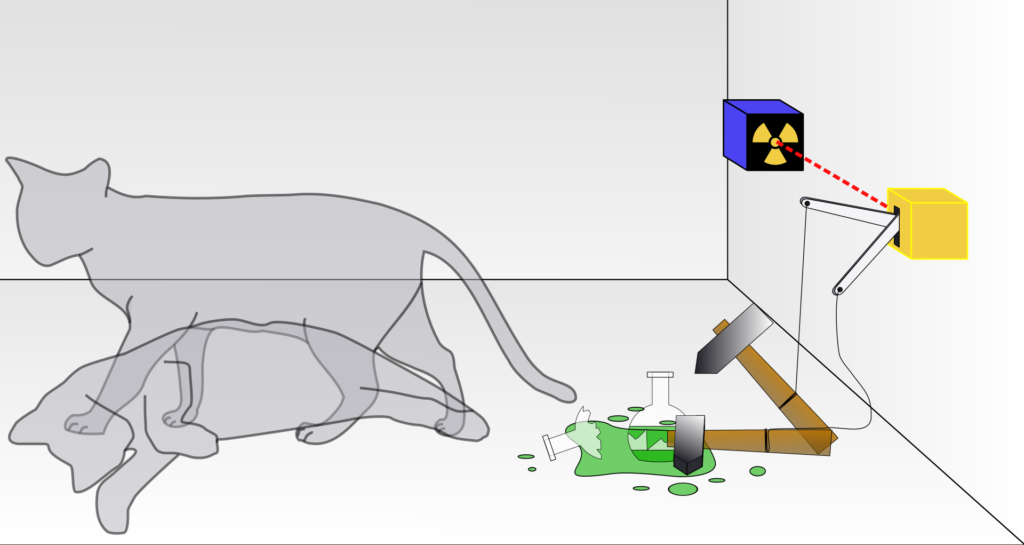

1935 yılında Erwin Schrödinger tarafından ortaya atılan “Schrödinger’in Kedisi” düşünce deneyi, kuantum mekaniğindeki süperpozisyon ilkesinin makroskopik sistemlere uygulanabilirliğini sorgular. Deneyde, bir kutunun içine yerleştirilmiş bir kedi, zehirli bir mekanizma, bir Geiger sayacı ve radyoaktif bir çekirdek bulunur. Çekirdeğin bozulup bozulmaması kuantum olasılık süreciyle belirlenir. Bozulma olursa zehirli mekanizma aktive olur ve kedi ölür. Ancak kutu açılmadıkça sistem bir süperpozisyon halinde kalır: kedi hem canlı hem ölü.
Bu durum, Kopenhag yorumu ile çağdaş yorumlar (Everett’in çoklu evren yorumu, pilot dalga teorisi vb.) arasındaki farklılıkları gözler önüne serer. Kimi yorumlar ölçüm eyleminin sistemin durumunu belirlediğini savunurken, kimileri evrenin tüm olası durumlarda dallandığını ileri sürer.
Formüllerin İsimleri ve Anlamları
| Sembol | İsim | Anlamı |
|---|---|---|
| i | İmajiner birim | Karmaşık sayıların temel birimi |
| ℏ | Planck sabiti (bölü 2π) | Kuantum eylem sabiti (reduced Planck constant) |
| ∂ | Kısmi türev | Zamana veya konuma göre değişim |
| t | Zaman | Sistemin zamana göre değişimini temsil eder |
| Ψ | Dalga fonksiyonu (zamanlı) | Kuantum sisteminin durumunu tanımlar |
| ψ | Dalga fonksiyonu (zamansız) | Sabit potansiyelde durum fonksiyonu |
| r | Konum | Uzaydaki yer bilgisi (vektörel konum) |
| H | Hamiltonyen operatör | Toplam enerji operatörü (kinetik + potansiyel) |
| m | Kütle | Parçacığın kütlesi |
| ∇2 | Laplace operatörü | İkinci dereceden mekansal türev |
| V | Potansiyel enerji fonksiyonu | Konuma bağlı enerji profili |
| λ | Dalga boyu | Parçacıkla ilişkili dalga uzunluğu |
| h | Planck sabiti | Evrensel fizik sabiti |
| p | Momentum | Parçacığın hareket miktarı |
| Δx | Konum belirsizliği | Parçacığın konumundaki ölçüm hassasiyeti |
| Δp | Momentum belirsizliği | Parçacığın momentumundaki ölçüm hassasiyeti |
| En | Enerji seviyesi | Belirli bir kuantum düzeyinin enerjisi |
| n | Kuantum sayısı | Enerji düzeylerini sayısal olarak gösterir |
| π | Pi sayısı | Matematiksel sabit (yaklaşık 3.1416, ama burada sayısal yok) |
| L | Uzunluk / Potansiyel kuyusu boyu | Sistem sınırı / sınırlayıcı kutunun genişliği |
| ω | Açısal frekans | Dairesel hareketin frekansı, harmonik osilatör için |
Schrödinger Denklemi: Matematiksel Temel ve Türevleri
Kuantum mekaniğinin temelini oluşturan Schrödinger Denklemi, bir sistemin dalga fonksiyonunun zamana göre evrimini belirler :
Bu denklem zamana bağlı Schrödinger Denklemi olarak bilinir.
Sabit potansiyel sistemlerde zamandan bağımsız hali kullanılabilir :
Bu durumda, ψ(r) enerjiye ait öz-fonksiyon, E ise o durumun enerjisini temsil eder.
Terimlerin Ayrıntılı Tanımları :
- Dalga fonksiyonu (Ψ) : Bir sistemin her konumda bulunma olasılığını belirleyen kompleks fonksiyondur. Karesi (|Ψ|²) olasılık yoğunluğudur.
- Hamiltonyen Operatör (Ĥ): Sistemin toplam enerjisini temsil eden operatördür. Genellikle kinetik ve potansiyel enerji terimlerinden oluşur :
Burada ∇² Laplace operatörü (ikinci türev), V(r) potansiyel enerji fonksiyonudur.
Dalga Mekaniği: Parçacık-Dalga Çiftliğinin Matematiksel İfadesi
Dalga mekaniği, Schrödinger denkleminin temelini oluşturduğu bir kuantum kuramıdır. Louis de Broglie tarafından öne sürülen madde dalgası kavramı, bir taneciğe “lambda = h / p” denklemiyle tanımlanır. Burada lambda dalga boyu, h Planck sabiti, p ise momentumdur.
Bu yaklaşım, taneciklerin klasik yörünge yerine olasılık dağılımıyla tanımlandığı bir fiziği öngörür. Belirsizlik ilkesi ise “” denklemle ifade edilir.
Bu da konum (x) ve momentum (p) hassasiyetlerinin sınırlı olduğunu gösterir.
Schrödinger Denklemi’nin Çözümleri ve Model Sistemler
Bazı klasik kuantum sistemleri:
- Kuantum Kuyusu: Sınırlı potansiyel kuyusunda enerji seviyeleri :
- Harmonik Osilatör :
- Hidrojen Atom Modeli :
Bu sistemlerde Schrödinger Denklemi analitik olarak çözülebilir ve enerji seviyeleri belirlenebilir.
Gerçek Hayat Uygulamaları
Schrödinger Denklemi kuantum teknolojilerinin kalbinde yer alır :
- Yarıiletken Fiziği: Transistör tasarımlarında bant yapısının belirlenmesinde.
- Kuantum Kimya: Moleküllerin elektron yapısını ve reaksiyon potansiyellerini hesaplamada.
- Kuantum Hesaplama: Qubit‘lerin evrimini ve kuantum algoritmalarını modellemede.
- Tıbbı Görüntüleme: Nükleer manyetik rezonans (NMR) teknikleri.
- Lazerler ve Atomik Saatler: Atom geçişleriyle hassas zaman ölçümü ve enerji salınımı.
- Malzeme Bilimi: Katı hal fiziğinde iletkenlik, manyetizma ve süper görüşlülük gibi olguların modellenmesi.
Yorumlar ve Felsefi Boyutlar
Schrödinger‘in Kedisi gibi düşünce deneyleri kuantum dünyası ile klasik gözlem dünyası arasındaki farklılıkları ortaya koyar. Kopenhag yorumuna göre sistem gözlem anında belirli hale gelir. Everett‘in çoklu evren yorumu ise her olasılığın farklı bir evrende gerçekleştiğini savunur.
Bu yorumlar, kuantum mekaniğinin temelinde yatan determinizm tartışmasını ve bilinmezlik ilkesiyle olan ilişkisini sorgular.